Transforming Finite State Automata into Regular Grammars

Algorithm

Given a finite state automaton with states Q (of which S is the start state and F is the set of final states), alphabet T and transition function t we would like to construct an equivalent regular grammar. Recall that to define a grammar we need to specify the set of terminals, the set of non-terminals, the start symbol and the set of production rules.

  1. The terminal alphabet of the grammar is defined to be T (the same as that of the automaton).
  2. The set of non-terminals is set to be Q -- the set of states of the automaton.
  3. The start symbol is S -- the start state of the automaton.
  4. Start with the empty set of production rules. For every transition (q,a)q' in t, add the production qaq'. If q' is a terminal state (in F) also add the production qa.
  5. If S is a terminal state (in F) add the production rule S.
  6. If the grammar is not epsilon-free, make it so (see relevant algorithm).

Note that all the productions introduced conform to the restrictions placed on regular grammar productions.

Example

Consider the finite state automaton M=< {S,A,B,C}, {a,b,c}, t, S, {S,C} > where t is the following set:

t = { (S,a)A,
(S,b)B,
(A,a)B,
(A,a)C,
(B,b)A,
(B,b)C,
(C,c)C}

Graphically, this automaton would appear as follows:

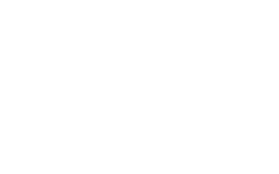
We will now construct an equivalent regular grammar. From steps 1, 2 and 3, we conclude that the terminal alphabet of the grammar is {a,b,c} and the non-terminal alphabet is {S,A,B,C}. The start symbol is the initial state S.

From every transition rule (q,a)q' we will now generate the production qaq':

S aA | bB,
A aB | aC,
B bA | bC,
C cC

For every production (q,a)q' where state q' is a final state in F, we will generate the production rule qa. We have only three such transitions: (A,a)C, (B,b)C and (C,c)C which will generate the following productions:

A a,
B b,
C c

Finally, since S is a terminal state, we also add the production S. The resultant set of production rules is thus:

S aA | bB | ,
A aB | aC | a,
B bA | bC | b,
C cC | c

Note that S does not appear anywhere on the right hand side of rules thus making the regular grammar -free.

Exercises

Give regular grammars equivalent to the following finite state automata: